Generative model의 한 종류인 VAE(Variational AutoEncoder)를 공부하기 전, 먼저 AE(AutoEncoder)에 대해서 간단하게 소개하려고 한다.
AE랑 VAE는 이름이 유사하지만, 목적은 아예 다르다.
AE는 원래 데이터를 복원하기 위해 Z를 잘 임베딩 하는 것(manifold learning)이 목적이며, VAE는 새로 만드는데 유사한 데이터로 재생성 하는 것이다.(generative model)
즉, AE (x => x) VAE (x => x')이다.
- Auto-Encoder
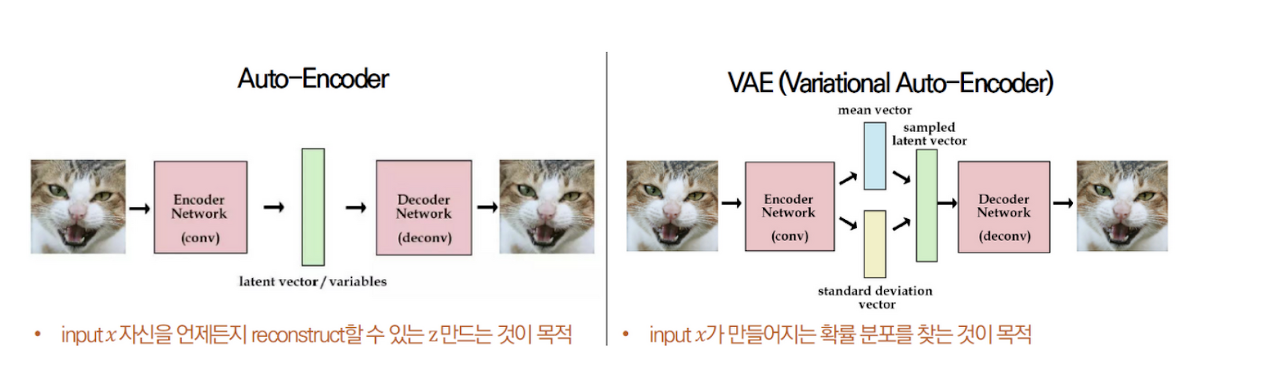
AE는 비지도 학습기반이며 인코더와 디코더로 구성되어 있다. 그런데 이름에도 나와있듯이, AE(AutoEncoder) 인코더에 집중한 방식이다. 입력을 받아서 효율적인 값(Latent Variable)으로 표현을 출력하고 싶은데, 이 Latent Variable의 값을 모르기 때문에 지도학습이 불가능하다. 그래서 이 Latent Variable 값을 구하기 위해서 디코더를 덧붙여서 학습을 하게 됐다고 할 수 있다.
인코더에서 Latent Variable를 생성하는데 원본 데이터가 압축이 되어 있는 형태라고 할 수 있다. 그래서 원본데이터를 차원축소했다고 생각할 수 있는데 (예: 통계기반방식 -> PCA) 그러면 신경망에서 내가 가지고 있는 원본 데이터를 차원 축소해서 이 원본 데이터가 가지고 있는 값을 잘 표현할 수 있도록 해야한다.
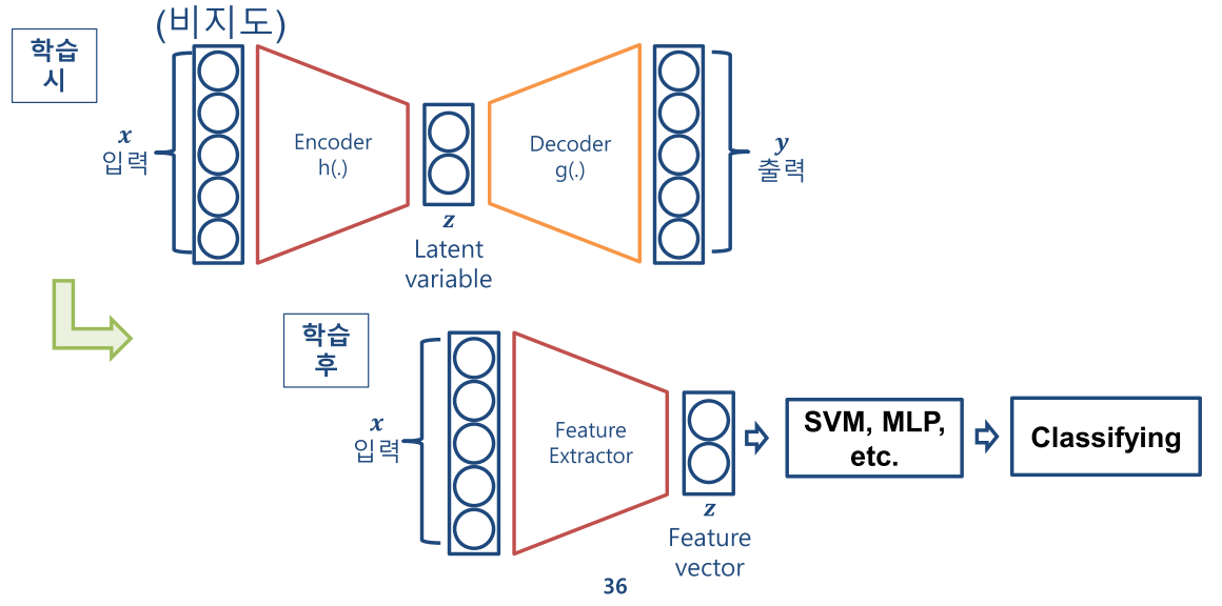
AE에서 인코더를 통과한 latent variable를 z라고 표현하겠다. 그래서 목표는 입력 데이터 x를 잘 압축하는 z를 생성하고 싶은데 이 z를 직접적으로 지도학습이 불가능하니, 이 z를 통해서 x와 유사한 형태의 값($\hat{x} $ )을 복원할 수 있는 신경망을 설계하는 것이다.
AE를 인코더 디코더를 하나의 신경망으로 보았을때, 입력과 출력의 x가 동일한 결과가 되도록 Loss가 최소화 되도록 학습이 된다. 그때 얻어지는 중간값이 z가 된다.
아까 앞에서 AE는 인코더에 집중한 모델이라고 했다. 그래서 학습이 완료된 후에는 디코더가 필요없다. 그리고 z를 가지고 원하는 Task에 입력으로 사용되는식으로 활용할 수 있다. (x => z => y)
- Variational Auto-Encoder
VAE는 GAN, Diffusion model과 같은 generative model의 한 종류로 입력 x와 유사한 새로운 데이터 \(x\)를 출력하는 것이 목적이다.
이를 위해서는 실제 data distribution인 \(p(x)\)를 approximate하는 것을 목표로 하며, AE와 거의 똑같은 구조 Encoder, Decoder, latent space로 구성된다.
새로운 데이터를 만드는 것은 유사한 형태의 데이터를 많이 보고 학습이 되어야 한다. 이미지로 예시를 들면 수많은 이미지를 보고 이미지들이(예 : 28 x 28 image) 가지고 있는 각각의 픽셀이 어떠한 패턴을 가지고 있는지 확률분포를 구해야한다. (보통 정규분포를 사용)

그러면 각 픽셀의 확률분포에서 하나의 점을 추출(sampling)한다면 새로운 데이터를 생성할 수 있는 것이다.
VAE는 AE와 다르게 디코더에 집중한 모델이라고 했다.
그래서 원래 VAE는 z에서 새로운 데이터를 추출하기 위해서 디코더만 필요로 한다.
그런데 z는 정규분포를 따른다고 할때, 이 z를 생성하기 위해서 정규분포를 구성하는 평균값(mu)과 표준편차(sigma) 를 만들 수 있는 인코더를 사용하기로 한 것이다. 이로써 AE와 목적은 다르나 구조상 동일하게 되어서 이름을 Variational AutoEncoder가 된 것이다.
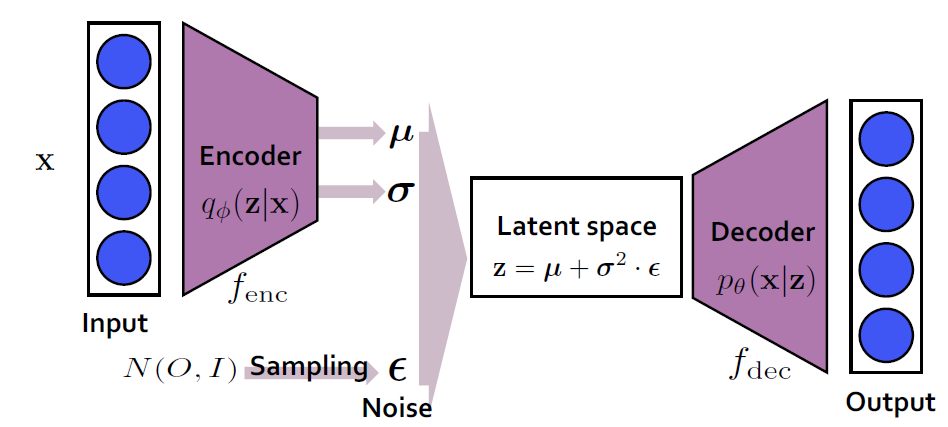
- Encoder
인코더는 입력 x를 latent space(잠재공간) z로 변환해주는 역할을 한다. 입력 데이터의 posterior, 달리 말하면 input x가 주어졌을 때 latent vector z의 분포, 위의 그림처럼 q(z|x)를 approximate하는 것을 목적으로 한다. 이 q(z|x)를 가장 잘 나타내는 분포로 정규분포를 선택한다면, q(z|x)를 approximate할 때는 정규분포의 핵심인 평균과 표준편차를 구하는 것이 그 목적이 된다.
- Decoder
Decoder는 encoder와 반대로 latent space를 input으로 변환하는 역할을 한다. 이 때, decoder는 input의 true distribution, 달리 말하면 latent vector z가 주어졌을 때 x의 분포, 즉 위 그림에서 나타나듯이 p(z|x)를 approximate하는 것을 목적으로 한다. 어떤 z라는 vector가 주어짐에 따라 다시 데이터 x를 generate하는 역할을 하기 때문에, decoder가 generative model의 역할을 하게 된다.
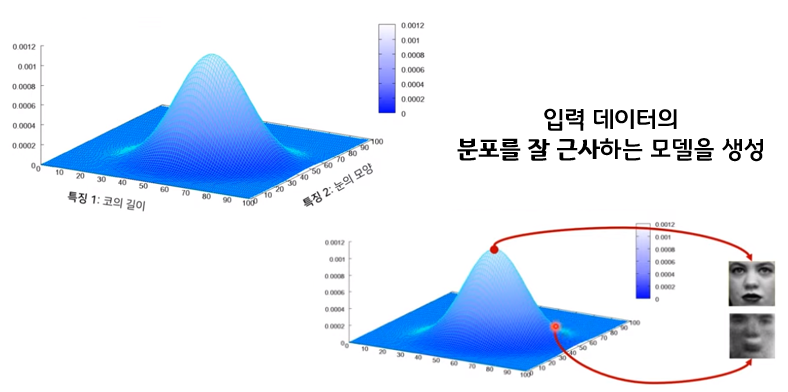
다시 정리하면, VAE는 input image가 들어오면 그 이미지에서의 다양한 특징들이 각각의 확률 변수가 되는 어떤 확률 분포를 만들게 되고, 이런 확률 분포를 잘 찾아내고, 확률값이 높은 부분을 이용하면 실제에 있을법한 이미지를 새롭게 만들 수 있다.
이제 VAE를 학습과정을 살펴보자, Loss function 대해서 설명하면, maximum likelihood(MLE) 접근법을 택한다. 즉, \($p_{theta}(x)\)를 maximize하는 theta를 찾는 것을 목적으로 하며, 이를 식으로 표현하면, 다음과 같은 loglikelihood를 maximize하는 것과 같다.
---------- 추가할 예정----------
2가지 Loss function의 합으로 표현된다.

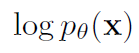
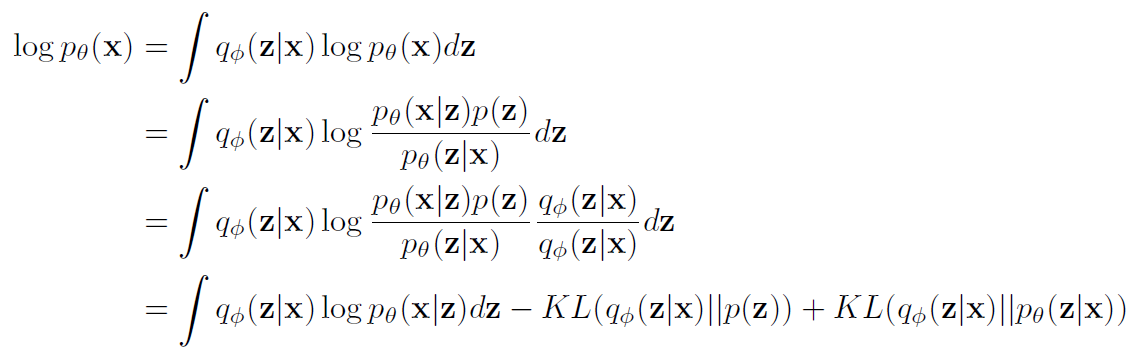
1) Reconstruction Error
- 현재 샘플링용 함수에 대한 negative log likelihood
- $x_i$ 에 대한 복원 오차 (AutoEncoder 관점)
2) Regularization Error
- 현재 샘플링용 함수에 대한 추가 조건
- 샘플링의 용의성/생성

VAE에서는 확률에 관련된 용어들이 많이 나온다. 아직 기초가 부족하다면 [1], [2], [4], [5] 링크를 참고하며 맨 밑에 용어들 참고
latent : ‘잠재하는’, ‘숨어있는’, ‘hidden’의 뜻을 가진 단어. 여기서 말하는 latent variable z는 특징(feature)를 가진 vector로 이해하면 좋다.
intractable : 문제를 해결하기 위해 필요한 시간이 문제의 크기에 따라 지수적으로 (exponential) 증가한다면 그 문제는 난해 (intractable) 하다고 한다.
explicit density model : 샘플링 모델의 구조(분포)를 명확히 정의
implicit density model : 샘플링 모델의 구조(분포)를 explicit하게 정의하지 않음
density estimation : x라는 데이터만 관찰할 수 있을 때, 관찰할 수 없는 x가 샘플된 확률밀도함수(probability density function)을 estimate하는 것
Gaussian distribution : 정규분포
Bernoulli distribution : 베르누이분포
Marginal Probability : 주변 확률 분포
D_kl : 쿨백-라이블러 발산(Kullback–Leibler divergence, KLD), 두 확률분포의 차이Encode / Decode: 암호화,부호화 / 암호화해제,부호화해제
likelihood : 가능도
[1] https://jjangjjong.tistory.com/41
[2] https://angeloyeo.github.io/2020/07/17/MLE.html
[3] https://wikidocs.net/152474
[4] https://taeu.github.io/paper/deeplearning-paper-vae/
[6] https://m.blog.naver.com/pmw9440/221519035437
6.2 R로 베이지안 추론 실시하기
0. 차례 1. 들어가기 2. 사전분포(Prior distribution)이란? 3. 사후분포(Posterior Distribution)란? 4...
blog.naver.com
통계랑 '4'일째: 확률변수와 모수 그리고 통계량
1. 들어가며 오늘은 두둥 드디어 수학 시간이 아니고 통계학 시간입니다. 사실 저번 시간까지 했던 것들은 전부 왠지 다 아는 것 같은데 저 사람이 뭔 소리하는 지 잘 모르겠던, 그런 시간이었죠?
stementor.tistory.com
[논문] VAE(Auto-Encoding Variational Bayes) 직관적 이해
VAE : Variational Auto-Encoder를 직관적으로 이해하기!
taeu.github.io
1) VAE(Variational Auto-Encoder)
## VAE란? VAE는 Input image X를 잘 설명하는 feature를 추출하여 Latent vector z에 담고, 이 Latent vector z를 통해 X와 유사하…
wikidocs.net
최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
'전체보기 > Generative Model' 카테고리의 다른 글
| Generative Model (0) | 2023.07.27 |
|---|
Generative model의 한 종류인 VAE(Variational AutoEncoder)를 공부하기 전, 먼저 AE(AutoEncoder)에 대해서 간단하게 소개하려고 한다.
AE랑 VAE는 이름이 유사하지만, 목적은 아예 다르다.
AE는 원래 데이터를 복원하기 위해 Z를 잘 임베딩 하는 것(manifold learning)이 목적이며, VAE는 새로 만드는데 유사한 데이터로 재생성 하는 것이다.(generative model)
즉, AE (x => x) VAE (x => x')이다.
- Auto-Encoder

AE는 비지도 학습기반이며 인코더와 디코더로 구성되어 있다. 그런데 이름에도 나와있듯이, AE(AutoEncoder) 인코더에 집중한 방식이다. 입력을 받아서 효율적인 값(Latent Variable)으로 표현을 출력하고 싶은데, 이 Latent Variable의 값을 모르기 때문에 지도학습이 불가능하다. 그래서 이 Latent Variable 값을 구하기 위해서 디코더를 덧붙여서 학습을 하게 됐다고 할 수 있다.
인코더에서 Latent Variable를 생성하는데 원본 데이터가 압축이 되어 있는 형태라고 할 수 있다. 그래서 원본데이터를 차원축소했다고 생각할 수 있는데 (예: 통계기반방식 -> PCA) 그러면 신경망에서 내가 가지고 있는 원본 데이터를 차원 축소해서 이 원본 데이터가 가지고 있는 값을 잘 표현할 수 있도록 해야한다.

AE에서 인코더를 통과한 latent variable를 z라고 표현하겠다. 그래서 목표는 입력 데이터 x를 잘 압축하는 z를 생성하고 싶은데 이 z를 직접적으로 지도학습이 불가능하니, 이 z를 통해서 x와 유사한 형태의 값($\hat{x} $ )을 복원할 수 있는 신경망을 설계하는 것이다.
AE를 인코더 디코더를 하나의 신경망으로 보았을때, 입력과 출력의 x가 동일한 결과가 되도록 Loss가 최소화 되도록 학습이 된다. 그때 얻어지는 중간값이 z가 된다.
아까 앞에서 AE는 인코더에 집중한 모델이라고 했다. 그래서 학습이 완료된 후에는 디코더가 필요없다. 그리고 z를 가지고 원하는 Task에 입력으로 사용되는식으로 활용할 수 있다. (x => z => y)
- Variational Auto-Encoder
VAE는 GAN, Diffusion model과 같은 generative model의 한 종류로 입력 x와 유사한 새로운 데이터 \(x\)를 출력하는 것이 목적이다.
이를 위해서는 실제 data distribution인 \(p(x)\)를 approximate하는 것을 목표로 하며, AE와 거의 똑같은 구조 Encoder, Decoder, latent space로 구성된다.
새로운 데이터를 만드는 것은 유사한 형태의 데이터를 많이 보고 학습이 되어야 한다. 이미지로 예시를 들면 수많은 이미지를 보고 이미지들이(예 : 28 x 28 image) 가지고 있는 각각의 픽셀이 어떠한 패턴을 가지고 있는지 확률분포를 구해야한다. (보통 정규분포를 사용)

그러면 각 픽셀의 확률분포에서 하나의 점을 추출(sampling)한다면 새로운 데이터를 생성할 수 있는 것이다.
VAE는 AE와 다르게 디코더에 집중한 모델이라고 했다.
그래서 원래 VAE는 z에서 새로운 데이터를 추출하기 위해서 디코더만 필요로 한다.
그런데 z는 정규분포를 따른다고 할때, 이 z를 생성하기 위해서 정규분포를 구성하는 평균값(mu)과 표준편차(sigma) 를 만들 수 있는 인코더를 사용하기로 한 것이다. 이로써 AE와 목적은 다르나 구조상 동일하게 되어서 이름을 Variational AutoEncoder가 된 것이다.

- Encoder
인코더는 입력 x를 latent space(잠재공간) z로 변환해주는 역할을 한다. 입력 데이터의 posterior, 달리 말하면 input x가 주어졌을 때 latent vector z의 분포, 위의 그림처럼 q(z|x)를 approximate하는 것을 목적으로 한다. 이 q(z|x)를 가장 잘 나타내는 분포로 정규분포를 선택한다면, q(z|x)를 approximate할 때는 정규분포의 핵심인 평균과 표준편차를 구하는 것이 그 목적이 된다.
- Decoder
Decoder는 encoder와 반대로 latent space를 input으로 변환하는 역할을 한다. 이 때, decoder는 input의 true distribution, 달리 말하면 latent vector z가 주어졌을 때 x의 분포, 즉 위 그림에서 나타나듯이 p(z|x)를 approximate하는 것을 목적으로 한다. 어떤 z라는 vector가 주어짐에 따라 다시 데이터 x를 generate하는 역할을 하기 때문에, decoder가 generative model의 역할을 하게 된다.

다시 정리하면, VAE는 input image가 들어오면 그 이미지에서의 다양한 특징들이 각각의 확률 변수가 되는 어떤 확률 분포를 만들게 되고, 이런 확률 분포를 잘 찾아내고, 확률값이 높은 부분을 이용하면 실제에 있을법한 이미지를 새롭게 만들 수 있다.
이제 VAE를 학습과정을 살펴보자, Loss function 대해서 설명하면, maximum likelihood(MLE) 접근법을 택한다. 즉, \($p_{theta}(x)\)를 maximize하는 theta를 찾는 것을 목적으로 하며, 이를 식으로 표현하면, 다음과 같은 loglikelihood를 maximize하는 것과 같다.
---------- 추가할 예정----------
2가지 Loss function의 합으로 표현된다.

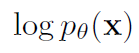
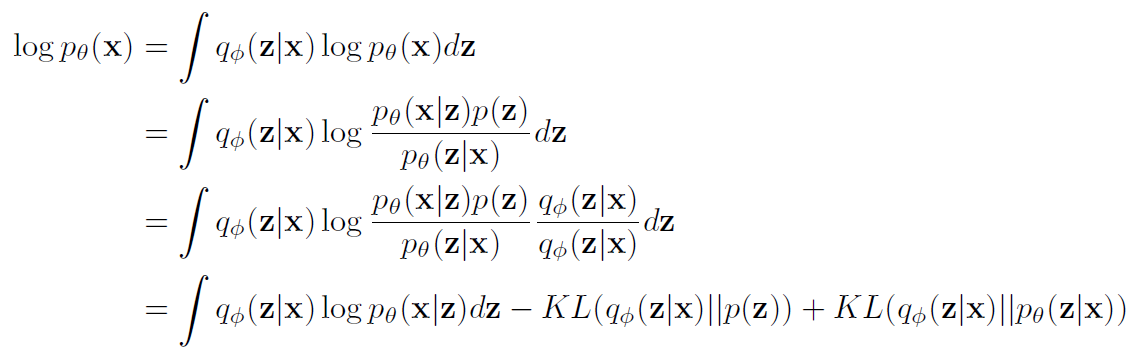
1) Reconstruction Error
- 현재 샘플링용 함수에 대한 negative log likelihood
- $x_i$ 에 대한 복원 오차 (AutoEncoder 관점)
2) Regularization Error
- 현재 샘플링용 함수에 대한 추가 조건
- 샘플링의 용의성/생성

VAE에서는 확률에 관련된 용어들이 많이 나온다. 아직 기초가 부족하다면 [1], [2], [4], [5] 링크를 참고하며 맨 밑에 용어들 참고
latent : ‘잠재하는’, ‘숨어있는’, ‘hidden’의 뜻을 가진 단어. 여기서 말하는 latent variable z는 특징(feature)를 가진 vector로 이해하면 좋다.
intractable : 문제를 해결하기 위해 필요한 시간이 문제의 크기에 따라 지수적으로 (exponential) 증가한다면 그 문제는 난해 (intractable) 하다고 한다.
explicit density model : 샘플링 모델의 구조(분포)를 명확히 정의
implicit density model : 샘플링 모델의 구조(분포)를 explicit하게 정의하지 않음
density estimation : x라는 데이터만 관찰할 수 있을 때, 관찰할 수 없는 x가 샘플된 확률밀도함수(probability density function)을 estimate하는 것
Gaussian distribution : 정규분포
Bernoulli distribution : 베르누이분포
Marginal Probability : 주변 확률 분포
D_kl : 쿨백-라이블러 발산(Kullback–Leibler divergence, KLD), 두 확률분포의 차이Encode / Decode: 암호화,부호화 / 암호화해제,부호화해제
likelihood : 가능도
[1] https://jjangjjong.tistory.com/41
[2] https://angeloyeo.github.io/2020/07/17/MLE.html
[3] https://wikidocs.net/152474
[4] https://taeu.github.io/paper/deeplearning-paper-vae/
[6] https://m.blog.naver.com/pmw9440/221519035437
6.2 R로 베이지안 추론 실시하기
0. 차례 1. 들어가기 2. 사전분포(Prior distribution)이란? 3. 사후분포(Posterior Distribution)란? 4...
blog.naver.com
통계랑 '4'일째: 확률변수와 모수 그리고 통계량
1. 들어가며 오늘은 두둥 드디어 수학 시간이 아니고 통계학 시간입니다. 사실 저번 시간까지 했던 것들은 전부 왠지 다 아는 것 같은데 저 사람이 뭔 소리하는 지 잘 모르겠던, 그런 시간이었죠?
stementor.tistory.com
[논문] VAE(Auto-Encoding Variational Bayes) 직관적 이해
VAE : Variational Auto-Encoder를 직관적으로 이해하기!
taeu.github.io
1) VAE(Variational Auto-Encoder)
## VAE란? VAE는 Input image X를 잘 설명하는 feature를 추출하여 Latent vector z에 담고, 이 Latent vector z를 통해 X와 유사하…
wikidocs.net
최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
'전체보기 > Generative Model' 카테고리의 다른 글
| Generative Model (0) | 2023.07.27 |
|---|